December 4th, Shmuel and the Pope

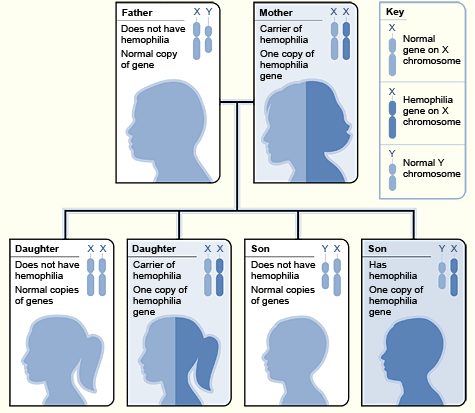
If you live in Israel, you need not read on.

December 4th is a significant day in the Jewish liturgical calendar. It is the day on which those who live outside Israel begin to add the words ותן טל ומטר - give us dew and rain. Here is the talmudic source for this change:

תענית דף י, א

משנה. בשלשה במרחשון שואלין את הגשמים. רבן גמליאל אומר: בשבעה בו, חמשה עשר יום אחר החג, כדי שיגיע אחרון שבישראל לנהר פרת

גמרא. אמר רבי אלעזר: הלכה כרבן גמליאל. תניא, חנניה אומר: ובגולה עד ששים בתקופה.

Mishnah: On the third of Marcheshvan we ask for rain [that is, we insert the words ותן טל ומטר into the Amidah prayer]. Rabban Gamliel said: it is started on the seventh.

Talmud: Said Rabbi Elazar, the law is like Rabban Gamliel. It was taught in a Beraita: Chaninah said: outside of Israel, it is inserted sixty days after the fall equinox.

This is the only Jewish ritual that is tied to a real solar event. That event is the autumnal equinox, the day on which the sun is directly overhead on the equator, and on which the lengths of day and night are (almost) equal.(Please do not write to tell me about Birkat Hachamah. It is not tied to any real solar or other event anywhere in the cosmos. See here for more details.)

This year the autumnal equinox was on September 22nd (at 9.54am EST to be precise). The Talmud tells us to begin saying ותן טלֹ sixty days later. So you take out the calendar and count. That will bring us to November 21st. But in every siddur with instructions you will read that we start to recite the addition at Maariv on the evening of December 4th. Which is tonight (or was last night if you are reading this in Australia). That’s a full seventy-three days after the equinox. How did that happen?

It is really not difficult to understand, and requires no skill in observational astronomy or non-Euclidian geometry. Here is the explanation in four easy steps.

1. The Julian Calendar

In the Julian calendar the solar year is exactly 365 1/4 days. That is, 365 days plus an additional 6 hours. This is also the length of the year according to the great talmudic sage of the second century, Samuel of Nehardea. And it is the assumed length of the solar year that is still used today in Jewish calculations. The actual length of the tropical year (i.e. one complete cycle of seasons) is slightly shorter: 365 days, 5 hours, 48 minutes and 46 seconds. That’s a difference of less than twelve minutes. Not much you say. And you’d be right, except that over a century that difference adds up to about 3/4 of a day. So every century the Julian calendar (365.25 days) falls behind the actual length of the year by three-quarters of a day.

2. The Gregorian Calendar

Over hundreds of years that difference adds up to many days, which became a real problem for the Church, when Easter was slipping further back in the calendar. The vernal equinox (a real solar event) had fallen on March 21st in the Julian calendar, but over the centuries had slipped back to March 11th. This threw the calculation of Easter into turmoil. To correct this (and other problems) Pope Gregory removed ten days from the calendar. By papal decree, the last day of the Julian calendar was on October 4, 1582. The next day became the first day of the Gregorian calendar, October 15, 1582. Now the spring equinox would fall on March 21, and everyone would be happy.

3. Jewish law stuck to the old Shmuel - Julian calendar

Rather than go along with this change, it was ignored by rabbis of the early modern period. They would rather have been wrong with Shmuel, than right with the Pope. They added back in the ten lost days. But by 1900 an additional three days of slippage had built up. The calendar of Shmuel is now some 13 missing days behind the Gregorian.

4. So add back in the missing days

If you add an additional thirteen days to the sixty days prescribed by the Talmud, you arrive at….December 4th! I told you it was easy. Here, try it for yourself:

Happy December 4th from Talmudology

Chullin 4b~ Circumcision, Shechita, and Hemophilia A

In tomorrow’s page of Talmud, we are deeply engrossed in the question of who is qualified to be a shochet, one who slaughters food in accordance with Jewish law. A baraita (a set of oral teachings that never quite made it into the Mishnah) is quoted that teaches that an uncircumcised man may be a shochet. Then the Talmud asks:

חולין ד, ב

ה"ד אילימא מתו אחיו מחמת מילה האי ישראל מעליא הוא אלא פשיטא מומר לערלות וקא סבר מומר לדבר אחד לא הוי מומר לכל התורה כולה

This uncircumcised man, what are the circumstances? If we say that he is an uncircumcised man whose brothers died due to circumcision and the concern is that he might suffer a similar fate, clearly he may slaughter, as he is a full-fledged Jew and not a transgressor at all. Rather, it is obvious that he is a transgressor with regard to remaining uncircumcised, as he refuses to be circumcised, and the tanna holds that he may nevertheless slaughter an animal since a transgressor concerning one matter is not a transgressor concerning the entire Torah.

The Talmud here is referring to the sad case in which a mother loses her sons because they bleed to death following circumcision. In this encore presentation, let’s revisit the topic, which we first met way back in Yevamot 64a.

יבמות סד, א

תניא מלה הראשון ומת שני ומת שלישי לא תמול דברי רבי רבן שמעון בן גמליאל אומר שלישי תמול רביעי לא תמול... א"ר יוחנן מעשה בארבע אחיות בצפורי שמלה ראשונה ומת שניה ומת שלישית ומת רביעית באת לפני רבן שמעון בן גמליאל אמר לה אל תמולי

It was taught: If she circumcised her first son and he died, and her second son and he too died, she should not circumcise her third son, so taught Rebbi.  Rabbi Shimon ben Gamliel stated that she should indeed circumcise her third child, but [if he died] she must not circumcise her fourth...Rabbi Yochanan said that there was once a case in Zippori in which four sisters had sons:  The first sister circumcised her son and he died, the second sister circumcised her son and he died, the third sister circumcised her son and he died, and the forth sister came to Rabbi Shimon ben Gamliel and he told her "you must not circumcise your son" (Yevamot 64a).

The Talmud here is describing a disease that is affected through the maternal line (hence the four sisters - all of whom seem to pass this disease on to their male children). The disease is X-linked Hemophilia A; the term X-linked indicates that the faulty gene is carried on the X chromosome, which is men is always inherited from the mother. Hemophilia A is an X-linked recessive genetic disease, first described by the American physician John Conrad Otto, who in 1803 described a bleeding disorder that ran in families and mostly affected the men. John Hay from Massachusetts published an account of a "remarkable hemorrhagic disposition" in the New England Journal of Medicine in 1813.

Hay, John. Account of a Remarkable Haemorrhagic Disposition, Existing in Many Individuals of the Same Family. New England Journal of Medicine 1813:2;3;221-225.

 If the mother is a carrier  - as were each of the four sisters in Zippori - then she has a one in four chance of passing on the disease to a child, and that affected child will always be a son:

Courtesy NHLBI

The rabbis argued over a technical point - that is, how many cases of bleeding are needed to establish a pattern. According to Rebbi (that is  Rebbi Yehuda Ha-Nasi, c. 135-217 CE.) two cases were sufficient, while Rabbi Shimon ben Gamliel insisted on three cases before ruling that there was a life threatening pattern.  Indeed the disease in boys must have been very perplexing, because (as you can see in the diagram above) not every boy would be affected. In fact, if the mother is a carrier and the father is not, there is only a 50% chance of a boy having hemophilia.  It is this fact that perhaps explains the dispute between Rebbi and Rabbi Shimon ben Gamliel regarding how many children need to exhibit the disease before we can assume that any future male child will also have it.  If every boy born in the family would have been a hemophiliac, Rabbi Shimon's ruling would have seemed unnecessarily cruel.  But since by chance, half of the boys born might not have hemophilia, the need to demonstrate the prevalence of the disease (in a society in which its genetic foundations were not known) seems eminently sensible.

In  Hemophilia A there are various genetic mutations that result in low levels of clotting factors. These levels may be only mildly decreased, or so low that severe life threatening hemophilia results. It is treated with transfusions of clotting factors which restore the levels to normal. Although these transfusions must be given several times a week in those with severe disease, there is hope that recombinant clotting factors can lengthen the time between the needed transfusions.

The hemophiliac as a shochet

The law discussed in Yevamot that forbids circumcision where there is a family history of hemophilia was certainly practiced. Later in Yevamot, the Mishnah records the case of a priest who was not circumcised -  because of the deaths of his brothers when they underwent the procedure. Tomorrow we read that a man who was not circumcised because he had hemophilia may serve as a shochet. The Talmud records not only the earliest known description of hemophilia, but the emphasis on the preservation of life as a normative Jewish practice. 

Menachot 110a ~ Free Will

In the Daf Yomi cycle, the last two tractates focussed on the laws of sacrifices. After a total of 230 double-sided pages we arrive at the last Mishnah on the topic (at least for now). It contains what is, scientifically, the most challenging statement in the entire Talmud.

מנחות קי, א

מתני׳ נאמר בעולת בהמה (ויקרא א, ט) אשה ריח ניחוח ובעולת עוף (ויקרא א, ט) אשה ריח ניחוח ובמנחה (ויקרא ב, ב) אשה ריח ניחוח לומר לך אחד המרבה ואחד הממעיט ובלבד שיכוין לבו לשמים

It is stated with regard to an animal burnt offering: “A fire offering, an aroma pleasing to the Lord” (Leviticus 1:9), and with regard to a bird burnt offering: “A fire offering, an aroma pleasing to the Lord” (Leviticus 1:17), and with regard to a meal offering: “A fire offering, an aroma pleasing to the Lord” (Leviticus 2:2). The repetitive language employed concerning all of these different offerings is to teach that the rewards for bringing a large or a small offering are the same so long as your intentions are for the sake of Heaven.

The Mishnah teaches us what was of ultimate importance when it comes to sacrifices. It is not the kind of sacrifice that was offered. Instead, it is the intention behind the offering. But what does intentionality - the ability to decide what to do or what not to do - what does that really mean? Does it even exist?

The Mechanical Universe

Consider the game of pool (for those outside the U.S. think about snooker). When I strike the white ball with my cue, it takes off down the green felt with a specific speed and direction. It strikes its target, say a red ball, at a specific angle and velocity, which then moves, hopefully into a pocket. It is clear that the movement of the red ball is caused by the movement of the white, which is caused by the movement of the cue. The red ball does not decide where to move. It is acted upon by an outside force. Were we to know the precise characteristics of that force, we could calculate where the ball would end up with 100% certainty. If the table were set up in the exact same way a second time, the same shot would result in the same outcome. That’s physics.

When my right thumb moves, it does so because the muscles to which it is attached contract in a certain way. And those muscles contract because the nerves that connect to them fired in a certain sequence. Those nerves fired because they received an electrical signal to do so from a neuron, or a group of neurons in the brain. And those neurons fired because other neurons in their vicinity did so. There is no magic here. They could not have done otherwise. It’s physics.

Since neurons only fire as a result of a stimulus, just where is the “deciding” neuron - the one that fires because you decide to move your thumb? The immutable laws of physics don’t allow for non-material thought to influence a material neuron. That would be as silly as trying to move the red ball by wishing it into the corner pocket. Our thoughts are contained in our brains which are made up of billions of firing neurons. Take away the neurons and you take away the thoughts. So what on earth do we mean when we say that we have decided to do something? There cannot have been any free will in that decision, because neurons are as predictable as billiard balls. Your decision to move your thumb may have felt like free will, but that freedom is an illusion.

Descartes and the Pineal Gland

The French philosopher Rene Descartes (1569-1650) was also troubled by the question of how the incorporeal mind (or what he termed the soul, but he meant the same thing) interacts with the material brain. He decided that the pineal gland, which lies deep inside the brain, was the place where physical brain and the soul meet:

The part of the body in which the soul directly exercises its functions is not the heart at all, or the whole of the brain. It is rather the innermost part of the brain, which is a certain very small gland situated in the middle of the brain’s substance and suspended above the passage through which the spirits in the brain’s anterior cavities communicate with those in its posterior cavities. …

So the soul, the part of us that dictates our thoughts and movements, is found inside the pineal gland, and from there it somehow influences our brains. It’s not much of a theory, as even Descartes acknowledged. In reply to question of how the soul moves the body if it is in no way material, he wrote that “the most ignorant people could, in a quarter of an hour, raise more questions of this kind than the wisest men could deal with in a lifetime; and this is why I have not bothered to answer any of them. These questions presuppose amongst other things an explanation of the union between the soul and the body, which I have not yet dealt with at all.” Yeah. So not helpful.

“The problem of free will and necessity is perhaps the most voluminously debated of all philosophical problems”

— Wallace Matson. A New History of Philosophy. New York, Harcourt Brace 1987. 158.

hard, soft and other flavors of determinism

Philosophers distinguish several kinds of determinism. Hard determinism is the belief that since all our actions are determined (see playing pool, above,) then free will does not exist in a sense required for genuine responsibility. In the words of the philosopher Derek Peereboom, this position involves “relinquishing our ordinary view of ourselves as blameworthy for immoral actions and praiseworthy for actions that are morally exemplary.” It also makes the notion of divine reward and punishment moot. Why would God punish you for an action which you could not otherwise have done? Or reward you for a good deed that you were equally predetermined to perform?

From the Talmudology Library Collection of books about free will. “עֲשׂוֹת סְפָרִים הַרְבֵּה אֵין קֵץ”

Soft determinism, also called compatibilism, is the belief that free will is compatible with determinism. This argument focuses not on physics and neuroscience but on linguistics, and what are known as Frankfurt cases. One argument, such as it is, goes like this. Suppose there is a man contentedly sitting in a room. He has no desire to leave, and if asked what he prefers to do, would answer that he wishes to stay in that room. We might say that he is sitting in the room of his own free will. But suppose that the door is locked and he has no power to open it. Is it still correct to say that he is sitting in the room of his own free will? If so, it does not follow that to have free will a person must be able to do otherwise than he does. It’s a neat philosophical trick, but soft determinism offers us no solution to the weighty challenge to the Jewish (and Christian) notions of reward and punishment, which is why the philosopher Henry James called it the “quagmire of evasion.”

Quantum Mechanics to the rescue?

Given the problem of determinism, some have reached out to quantum mechanics to preserve some modicum of free will. It’s true, they say, that our minds must have a physical basis, and that as such our minds are subject to the same laws of physics as are billiard balls. That is true on a macro level, but quantum mechanics teaches us that at an atomic level there is an indeterminacy that allows for free will to emerge. This argument was recently re-suggested by Nathan Aviezer, in Hakirah, The Flatbush Journal of Jewish Law and Thought. Aviezer, a Professor of Physics and former Chairman of the Physics Department of Bar-Ilan University, discussed quantum mechanics, the theory that position of atomic and subatomic particles can only be described in a probabilistic way. “The probabilistic nature of quantum mechanics” he wrote, “leads to an important conclusion that is easily stated: the present does not determine the future.” Then this:

We have previously explained that the behavior of individual atoms lies within the quantum level. Thus, quantum theory may indeed play an essential role in the thought process. How the workings of the brain are translated into the sensations and thoughts of the conscious mind is still shrouded in deep mystery. Nevertheless, it appears that the process of thinking cannot be described within the framework of classical physics, and quantum theory may have to be invoked. This is sufficient to disprove…[the] claim of the scientific impossibility of free will.

Well, if only it was that easy. There are at least four problems with the “quantum theory saves us from determinism” argument. They’re not mine, but belong to Prof. Robert Kane, author of The Significance of Free Will and editor of (one of my favorite books on the topic,) The Oxford Handbook of Free Will.

1. There has been, and continues to be considerable debate about the conceptual foundations of quantum physics and much disagreement about how it is to be interpreted.

2. Even if the behavior of elementary particles is not determined, this has no bearing on the question of free will, since quantum indeterminacy is not important at the level of macroscopic physical systems like human brains. (A single neuron is known to be excited by as many as twenty thousand molecules, each consisting of ten to twenty atoms. Although quantum effects may act on a single atom, they do not affect large numbers of atoms.)

3. Even if quantum effects had an effect on the brain as a whole, this is of no help to those (like Prof. Aviezer) who defend the existence of free will. In this case, a person’s free will boils down to the random movement of a few elementary particles. “Such undetermined effects” writes Prof. Kane, “ would be unpredictable and uncontrollable by the agents, like the unanticipated emergence of a thought or the uncontrolled jerking of an arm, - just the opposite of the way we envision free and responsible actions.”

4. Although determinism in basic physics has taken a retreat, evidence for determinism in sciences other than physics, like neuroscience, biology, genetics, psychiatry and the social and behavioral sciences has actually increased enormously over the last few decades. And they all point to the fact that our behavior is often the result of our genes, our evolutionary history, or our social and cultural conditioning.

Echoing Kane’s last point, here is what I wrote several years ago in my book that discussed the impact of Copernican thought on Judaism:

Over the last fifty years, advances in neuroscience have raised deep and weighty questions about what it means to think and act with free will. We have come to understand that our states of mind are more determined than we had ever imagined. Consider, for example, the common affliction of depression. We now have an understanding of its biochemical basis, and as a result, it is possible to successfully treat this disease with medication. Furthermore, the genetic basis of a vast number of other disorders once classified under the general and imprecise umbrella of “mental disorders” has been determined. It would seem that the way we feel or interact with others is not volitional, but is in large part predetermined by the genes we inherit. This genetic basis of much of our behavior may even affect our ability to make moral decisions. There is evidence that criminal behavior may not only be the result of personal choice, but may be genetically programmed from conception. All this evidence suggests that perhaps we cannot act otherwise than we do. The religious thinker must grapple with the question of what this implies for concepts that are central to the major world religions, such as freedom of choice, sin, and repentance. What role do Yom Kippur and Lent play in seeking God’s forgiveness if we are never able to do otherwise than sin? What becomes of the concept of reward in the afterlife if our actions on Earth are never freely made? It is questions like these that are the basis of a new interest in the way in which scientific discoveries affect religious sensibilities.

The Experiments of Benjamin Libet

Benjamin Libet (1916-2007), the son of Ukrainian Jewish immigrants was one of the leading neuroscientists of his day, and of all the work he did (see the second book from the bottom in the photo above), it is his experiments in the area of free will and consciousness for which he is best remembered. He discovered that our decisions to act are made long before (in scientific time) we are conscious of having made them. He connected his subjects to an EEG machine, and then asked them to tap a button whenever they decided. He also asked them to look at the moving dot on the oscilloscope timer and note its position at the time they first became aware of their decision to press that button. He compared the marked time of the button's pushing and the EEG recordings, and found something remarkable. The recorded brain activity that said “push the button” occurred as many as three hundred milliseconds before subjects reported the first awareness of their conscious decision to act. The upshot means that our conscious decisions to act are actually preceded by an subconscious buildup of electrical activity within the brain.

More recently, work by Itzhak Fried at Tel Aviv Medical Center and the Sackler School of Medicine demonstrated that individual neurons fire about two full seconds before a reported decision to act, and long before EEG activity showed such a response. “The scientific, philosophical, and societal implications of these findings” wrote Fried, “remain open for debate.”

Copernicus, Darwin, Libet and a prediction

Our understanding of the biochemical basis of our behaviors, whether based on genetics or neuropharmacology, is also challenging some of the traditional Jewish notions of free will and responsibility. In so doing, science raises a set of difficulties at least as troubling as those raised five hundred years ago when Copernicus suggested that the Earth was not the stationary center of the universe. In fact, when properly understood, this challenge is far more threatening to truly important foundational Jewish beliefs than was the discussion of whether or not the Earth moves. How will Jewish thinkers respond to this most recent and important religious challenge to arise from the scientific community?

Judaism, (like Christianity and Islam) will need to provide its adherents with a religiously satisfying way to address issues that are raised by these and other exciting findings. The history of the Jewish reception of Copernican thought suggests that both secular scientists and the religiously observant might have room to be optimistic. Jews eventually found a way to incorporate what was a very disconcerting hypothesis (we are not the center of the universe) into a religiously acceptable fact. It took hundreds of years, and there were some detours and backtracks along the way. But some five hundred years after Copernicus lived, a Jew whose faith is challenged by the notion that the Earth revolves around the Sun is a rare creature indeed. A similar pattern is already being seen as Jews grapple with the theological implications of Darwinian evolution.

This is what will happen. Although initially there will be some Jews who will see no problem reconciling a physical or biochemical basis of human behavior with traditional Jewish teachings on free will and personal responsibility, at first, Jewish thinkers will overwhelmingly write against it. They will maintain that such a theory stands in opposition to a number of biblical verses, and will further claim that in any event, the theory is scientifically flawed for reasons that are clear to them, but somehow opaque to those scientists actually involved in the research. After a number of years (perhaps even several decades), and assuming that more scientific evidence accumulates to support the theory, the tide will slowly turn in favor of a religious accommodation. Eventually, the overwhelming majority of Jews (at least those for whom such things matter) will accept that there is no conflict between the biochemical-determinist explanations of human behavior and Jewish thought that holds us accountable for our actions. They will claim that traditional sources, when properly understood, can be interpreted in a way that lends support to their inclusive approach. That’s what I predict. I can do no other.

Mencahot 106a ~ Gauss, Tosafot, and the Sum of Consecutive Numbers

A mincha offering is accompanied by a minimum of a one-issaron measure of flour. But a mincha can also be accompanied by a multiple of that number, up to a maximum of 60 issronot. What happens if a person vows to bring a specific number of isranot of flour to accompany a mincha offering but cannot recall how many he had in mind? What number of issronot of flour should he offer? Well it’s a bit tricky. The sages ruled that a single offering using the full sixty issronot of flour is all that needs to be brought. But the great editor of the Mishnah, Rabbi Yehudah Hanasi disagreed. In a spectacular way. Here is the discussion in tomorrow’s page of Talmud:

מנחות קו, א

תנו רבנן פירשתי מנחה וקבעתי בכלי אחד של עשרונים ואיני יודע מה פירשתי יביא מנחה של ששים עשרונים דברי חכמים רבי אומר יביא מנחות של עשרונים מאחד ועד ששים שהן אלף ושמונה מאות ושלשים

The Sages taught in a baraita: If someone says: I specified that I would bring a meal offering, and I declared that they must be brought in one vessel of tenths of an ephah, but I do not know what number of tenths I specified, he must bring one meal offering of sixty-tenths of an ephah. This is the statement of the Rabbis. Rabbi Yehuda HaNasi says: He must bring sixty meal offerings of tenths in sixty vessels, each containing an amount from one-tenth until sixty-tenths, which are in total 1,830 tenths of an ephah.

Since there is a doubt as to the true intentions of the vow, Rabbi Yehudah HaNasi covers all the bases and requires that every possible combination of a mincha offering be brought. So you start with one mincha offering accompanied with one issaron of flour, then you bring a second mincha offering accompanied with two issronot of flour, then you bring a third mincha together with three issronot, and so on until you reach the maximum number of issronot that can accompany the mincha - that is until you reach sixty. How many is that in total? In tomorrow’s page of Talmud the total number of Rabbi Yehudah HaNasi’s mincha offerings is calculated: 1,830.

How did the Talmud arrive at that number? We are not told, and presumably you simply add up the series of numbers 1+2+3+4….+59+60, which gives a total of 1,830. That certainly would work. But Tosafot offers a neat mathematical trick to figure out the sum of a mathematical sequence like this:

שהן אלף ושמונה מאות ושלשים. כיצד קח בידך מאחד ועד ששים וצרף תחילתן לסופן עד האמצע כגון אחד וששים הם ס"א שנים ונ"ט הם ס"א ושלש ונ"ח הם ס"א כן תמנה עד שלשים דשלשים ושלשים ואחד נמי הם ס"א ויעלה לך שלשים פעמים ס"א וכן נוכל למנות פרים דחג דעולין לשבעים כיצד ז' וי"ג הם עשרים וכן ח' וי"ב הם עשרים וכן ט' וי"א הם כ' וי' הרי שבעים

How did we arrive at 1,830? Take the series from 1 to 60 and add the sum of the first to the last until you get to the middle. Like this: 1+60=61; 2+59=61; 3+58=61. Continue this sequence until you get to 30+31 which is also 61. You will have 30 sets of 61 (ie 1,830). This method may also be used to count the number of sacrificial bulls on Sukkot, which are a total of 70. How so? [There are thirteen offered on the first day of sukkot, and one fewer bull is subtracted each day until the last day of sukkot, on which seven bulls are offered.] 13+7=20; 12+8=20; 11+9=20… [There are a total of 3 pairs of 20+ an unpairable 10]= 70.

In mathematical terms, the Tosafot formula for the sum (S) of the consecutive numbers in Rebbi’s series, where n is the number of terms in the series and P is the largest value, is S= n(P+1)/2. Which reminds us of…

Carl Friedrich Gauss

Carl Friedrich Gauss (1777-1855) was one of the world’s greatest mathematicians. He invented a way to calculate the date of Easter (which is a lot harder than you’d think), and made major contributions to the fields of number theory and probability theory. He gave us the Gaussian distribution (which you might know as the ”bell curve”) and used his skills as a mathematician to locate the dwarf planet Ceres. The British mathematician Henry John Smith wrote about him that other than Isaac Newton, “no mathematicians of any age or country have ever surpassed Gauss in the combination of an abundant fertility of invention with an absolute rigorousness in demonstration, which the ancient Greeks themselves might have envied.”

There is a delightful (though possibly apocryphal) story about Gauss as a bored ten-year old sitting in the class of Herr Buttner, his mathematics teacher. Here it is, as told by Tord Hall in his biography of Gauss:

When Gauss was about ten years old and was attending the arithmetic class, Buttner asked the following twister of his pupils. “Write down all the whole numbers from 1 to 100 and add their sum…The problem is not difficult for a person familiar with arithmetic progressions, but the boys were still at the beginner’s level, and Buttner certainly thought that he would be able to take it easy for a good while. But he thought wrong. In a few seconds, Gauss his slate on the table, and at the same time he said in his Braunschweig dialect: “Ligget se” (there it lies). While the other pupils added until their brows began to sweat, Gauss sat calm and still, undisturbed by Buttner’s scornful or suspicious glances.

How had the child prodigy solved the puzzle so quickly? He had added the first number (1) to the last number (100), the second number (2) to the second from last number (99) and so on. Just like Tosafot suggested. The sum of each pair was 101 and there were 50 pairs. And so Gauss write the answer on his slate board and handed it to Herr Buttner. It is 5,050.

…and now for some homework

Gauss was raised as a Lutheran in the Protestant Church, and so he did not learn of this method from reading Tosafot. But it is delightful to learn that the same mathematical solution that launched Gauss into his career as a mathematician can be found on page 106a of Menachot. With Chanukah just a few days away, can you calculate how many candles in total you need to light using the Gaussian-Tosafot method?