A mincha offering is accompanied by a minimum of a one-issaron measure of flour. But a mincha can also be accompanied by a multiple of that number, up to a maximum of 60 issronot. What happens if a person vows to bring a specific number of isranot of flour to accompany a mincha offering but cannot recall how many he had in mind? What number of issronot of flour should he offer? Well it’s a bit tricky. The sages ruled that a single offering using the full sixty issronot of flour is all that needs to be brought. But the great editor of the Mishnah, Rabbi Yehudah Hanasi disagreed. In a spectacular way. Here is the discussion in tomorrow’s page of Talmud:
מנחות קו, א
תנו רבנן פירשתי מנחה וקבעתי בכלי אחד של עשרונים ואיני יודע מה פירשתי יביא מנחה של ששים עשרונים דברי חכמים רבי אומר יביא מנחות של עשרונים מאחד ועד ששים שהן אלף ושמונה מאות ושלשים
The Sages taught in a baraita: If someone says: I specified that I would bring a meal offering, and I declared that they must be brought in one vessel of tenths of an ephah, but I do not know what number of tenths I specified, he must bring one meal offering of sixty-tenths of an ephah. This is the statement of the Rabbis. Rabbi Yehuda HaNasi says: He must bring sixty meal offerings of tenths in sixty vessels, each containing an amount from one-tenth until sixty-tenths, which are in total 1,830 tenths of an ephah.
Since there is a doubt as to the true intentions of the vow, Rabbi Yehudah HaNasi covers all the bases and requires that every possible combination of a mincha offering be brought. So you start with one mincha offering accompanied with one issaron of flour, then you bring a second mincha offering accompanied with two issronot of flour, then you bring a third mincha together with three issronot, and so on until you reach the maximum number of issronot that can accompany the mincha - that is until you reach sixty. How many is that in total? In tomorrow’s page of Talmud the total number of Rabbi Yehudah HaNasi’s mincha offerings is calculated: 1,830.
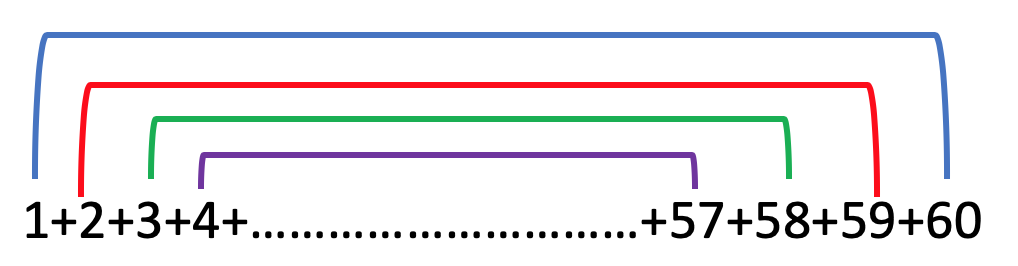
How did the Talmud arrive at that number? We are not told, and presumably you simply add up the series of numbers 1+2+3+4….+59+60, which gives a total of 1,830. That certainly would work. But Tosafot offers a neat mathematical trick to figure out the sum of a mathematical sequence like this:
שהן אלף ושמונה מאות ושלשים. כיצד קח בידך מאחד ועד ששים וצרף תחילתן לסופן עד האמצע כגון אחד וששים הם ס"א שנים ונ"ט הם ס"א ושלש ונ"ח הם ס"א כן תמנה עד שלשים דשלשים ושלשים ואחד נמי הם ס"א ויעלה לך שלשים פעמים ס"א וכן נוכל למנות פרים דחג דעולין לשבעים כיצד ז' וי"ג הם עשרים וכן ח' וי"ב הם עשרים וכן ט' וי"א הם כ' וי' הרי שבעים
How did we arrive at 1,830? Take the series from 1 to 60 and add the sum of the first to the last until you get to the middle. Like this: 1+60=61; 2+59=61; 3+58=61. Continue this sequence until you get to 30+31 which is also 61. You will have 30 sets of 61 (ie 1,830). This method may also be used to count the number of sacrificial bulls on Sukkot, which are a total of 70. How so? [There are thirteen offered on the first day of sukkot, and one fewer bull is subtracted each day until the last day of sukkot, on which seven bulls are offered.] 13+7=20; 12+8=20; 11+9=20… [There are a total of 3 pairs of 20+ an unpairable 10]= 70.
In mathematical terms, the Tosafot formula for the sum (S) of the consecutive numbers in Rebbi’s series, where n is the number of terms in the series and P is the largest value, is S= n(P+1)/2. Which reminds us of…
Carl Friedrich Gauss
Carl Friedrich Gauss (1777-1855) was one of the world’s greatest mathematicians. He invented a way to calculate the date of Easter (which is a lot harder than you’d think), and made major contributions to the fields of number theory and probability theory. He gave us the Gaussian distribution (which you might know as the ”bell curve”) and used his skills as a mathematician to locate the dwarf planet Ceres. The British mathematician Henry John Smith wrote about him that other than Isaac Newton, “no mathematicians of any age or country have ever surpassed Gauss in the combination of an abundant fertility of invention with an absolute rigorousness in demonstration, which the ancient Greeks themselves might have envied.”
There is a delightful (though possibly apocryphal) story about Gauss as a bored ten-year old sitting in the class of Herr Buttner, his mathematics teacher. Here it is, as told by Tord Hall in his biography of Gauss:
When Gauss was about ten years old and was attending the arithmetic class, Buttner asked the following twister of his pupils. “Write down all the whole numbers from 1 to 100 and add their sum…The problem is not difficult for a person familiar with arithmetic progressions, but the boys were still at the beginner’s level, and Buttner certainly thought that he would be able to take it easy for a good while. But he thought wrong. In a few seconds, Gauss his slate on the table, and at the same time he said in his Braunschweig dialect: “Ligget se” (there it lies). While the other pupils added until their brows began to sweat, Gauss sat calm and still, undisturbed by Buttner’s scornful or suspicious glances.
How had the child prodigy solved the puzzle so quickly? He had added the first number (1) to the last number (100), the second number (2) to the second from last number (99) and so on. Just like Tosafot suggested. The sum of each pair was 101 and there were 50 pairs. And so Gauss write the answer on his slate board and handed it to Herr Buttner. It is 5,050.
…and now for some homework
Gauss was raised as a Lutheran in the Protestant Church, and so he did not learn of this method from reading Tosafot. But it is delightful to learn that the same mathematical solution that launched Gauss into his career as a mathematician can be found on page 106a of Menachot. With Chanukah just a few days away, can you calculate how many candles in total you need to light using the Gaussian-Tosafot method?